Overview
WarpX simulates the self-consistent evolution of particle species (e.g., electrons, ions, etc.) in the presence of electric and magnetic fields. In this context, self-consistent indicates that the particle dynamics are influenced by the fields, while the fields themselves evolve in response to the particles’ changing charge and current densities.
The fields are represented on a discrete spatial grid (see Grid & Geometries). The species are most commonly represented by discrete macroparticles moving continuously through the grid, but can also be represented as fluids discretized on a grid (see Species Representations).
At each time step of a simulation, both the species and the fields are updated – using the equations of motion and the field equations respectively. More specifically, the following operations are performed at each time step, as represented in the figure below:
The electric and magnetic fields are interpolated from the grid to the macroparticles (or to the nodes of the fluid grid, for species represented as fluids)
These fields are used in the equation of motion to update the macroparticles’ position and momentum (or the fluid density and velocity)
The species deposit their charge density and/or current density onto the grid.
The fields are updated on the grid using the field equations, with the charge and/or current density as source terms.
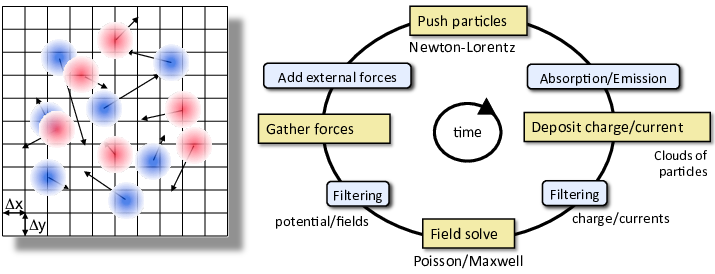
Fig. 33 Schematic high-level representation of the Particle-In-Cell (PIC) algorithm.
In WarpX, different types of field equations can be used to update the fields (e.g., Maxwell’s equations for fully-electromagnetic field update, Poisson equation for electrostatic field update, etc.). This choice – and the choice of a corresponding field solver – determine many of the algorithmic details of the above loop (see Models & Algorithms), such as the maximum time step size, the exact time-stepping algorithm, and whether the species’ charge density or current density is used.